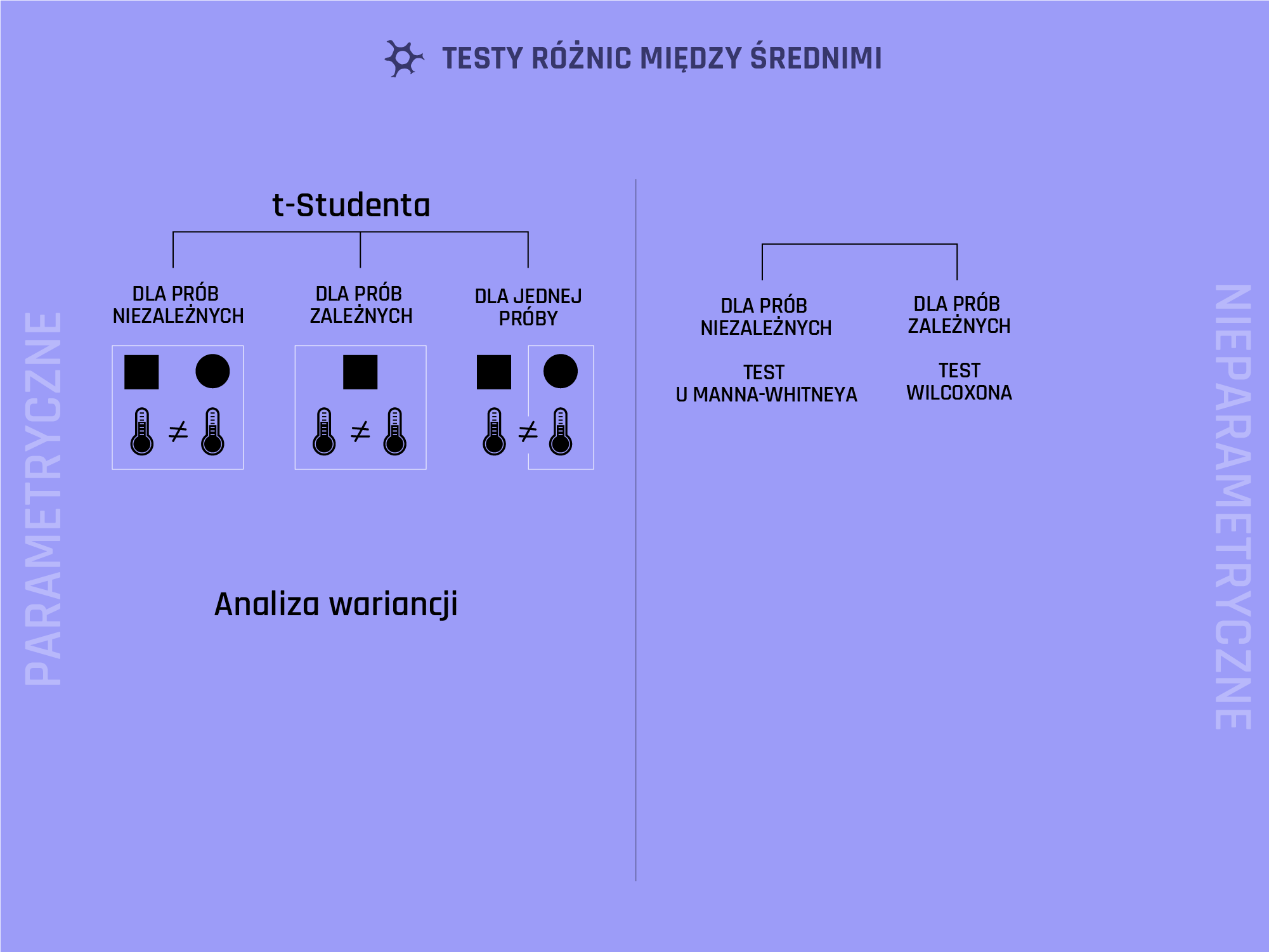
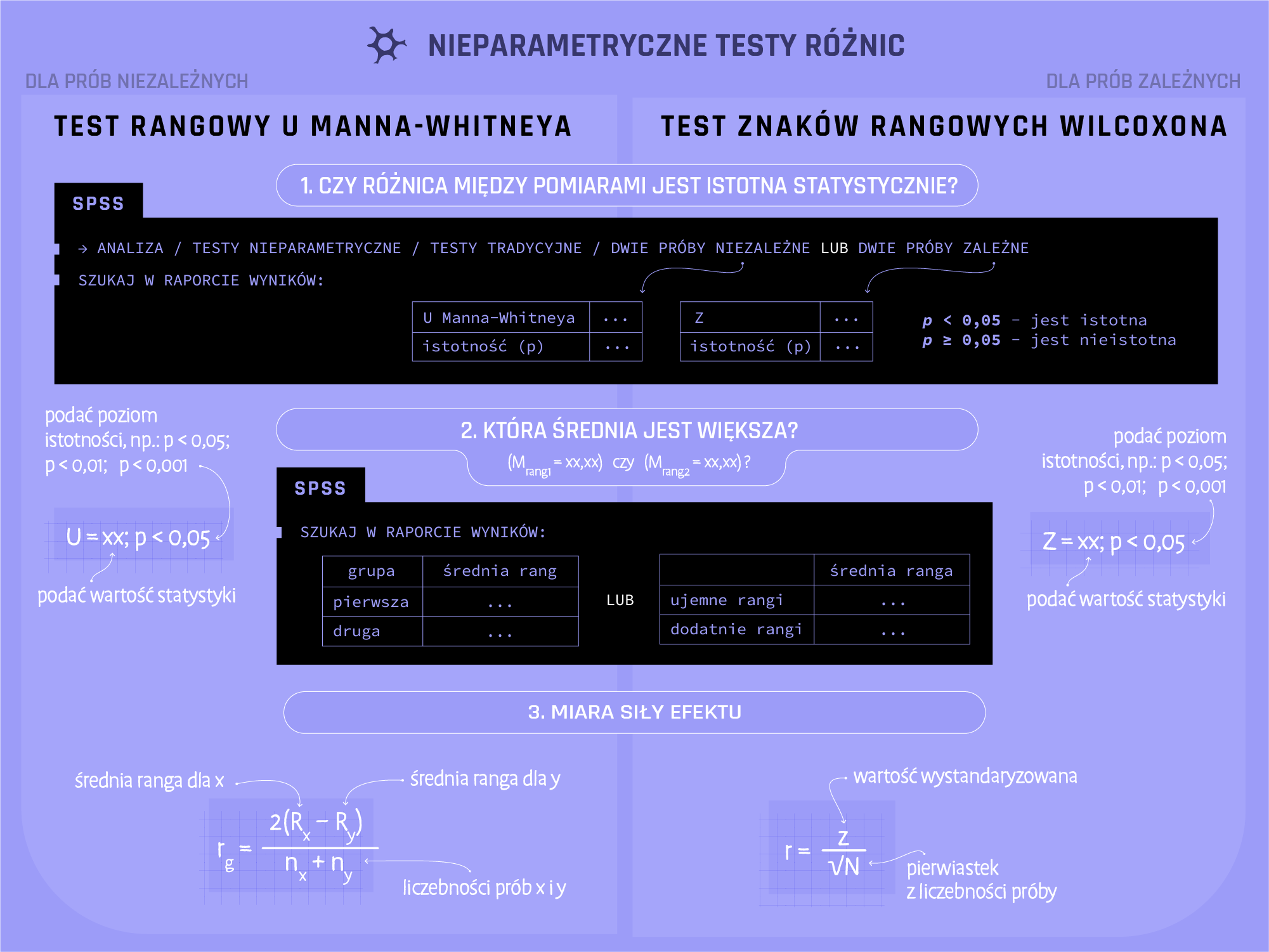
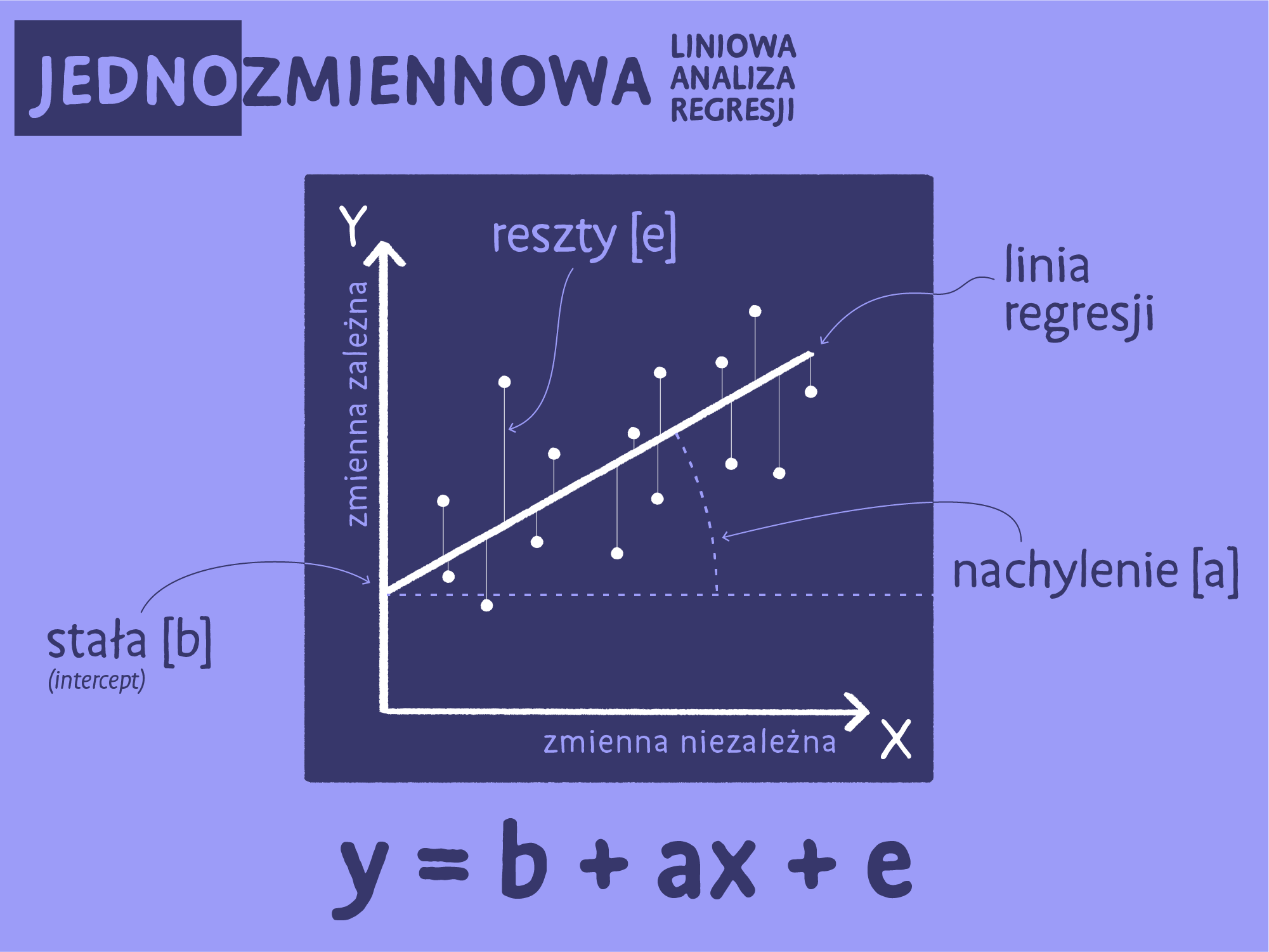
Obliczanie analizy regresji w SPSS
-> Analiza/Regresja/Liniowa
Uzupełniamy zmienną zależną i zmienne niezależne (w regresji wielozmiennowej wrzuca się tu kilka predyktorów).
Statystyki:
dopasowanie modelu,
oszacowania,
stat opisowe,
korelacje cząstkowe i semicząstkowe,
test współliniowości (tolerancja i VIF)
ewentualnie:
Wykresy: ZPRED-> X, ZRESID -> Y i histogram i normal p plot i partial plots
ZAPISZ: Cook's distance
-> Raport wyników:
1. Tabela korelacji:
patrzymy na korelacje między predyktorami (nie chcemy duyżych) jeśli są większe niż 0,7, to niedobrze i lepiej nie robić regresji liniowej.
Chcemy też, żeby zmienna zależna korelowała z predyktorami (musi być związek liniowy między nimi) - najlepiej by była to korelacja większa niż 0,3.
2. Tabela ANOVA:
jeśli jest istotne F, to model regresji pozwala lepiej przewidywać wyniki zmiennej zależnej niż średnia
- czyli model, w którym predyktorami są zmienne x1 i x2 i (xn) istotnie wyjaśnia zmienną y.
3. Tabela współczynników:
Pożądanymi wartościami dla Tolerancji i VIF są wartości blisko 1.
4. tabela Statystyki reszt (residuals statistics)
szukam standard residual (chcemy, żeby min i max nie przekraczały od -3 do 3),
odległość Cooka - max 1
5. Tabela z podsumowaniem wyników:
Interpretujemy wyjaśnioną wariancję: jaki procent wariancji zmiennej zależnej jest wyjaśniany przez predyktory
(jaka jest efektywność modelu): R2 lub skorygowane R2 (dla regresji wielozmiennowej).
Korelacje czątkowe i semicząstkowe wyjaśniają unikatowy wkład każdego predyktora.
Jeśli korelacje semicząstkowe (ang. part) podniesie się do kwadratu i pomnoży przez 100%, uzyska się procent wariancji
zmiennej zależnej, który jest wyjaśniony wyłącznie przez dany predyktor.
Zero-order correlation - ma w sobie oprócz wariancji predyktora, jeszcze tą cząstkę współdzieloną z drugim predyktorem.
Cząstkowa korelacja (ang. partial) informuje o tym, ile wariancji wyjaśnia cały jeden predyktor
(łącznie z tym co nachodzi na drugi predyktor).
6. Tabela Współczynniki:
Tu są dokładne informacje o tym, które zmienne wyjaśniające (predyktory) pozawalają przewidywać (i w jaki sposób)
zmienną zależną: zmienne niestandar. będą użyte w równaniu:
Stała/b0 - przewidywana wartość zmiennej zależnej, dla której wartość predyktora wynosi zero.
Współczynnik B/b1/a (drugi wiersz w tabeli) - nachylenie prostej względem osi X (jak szybko zmieniają się wartości zmiennej zależnej, jeśli wartość predyktora wzrośnie o 1 punkt).
Współczynnik Beta (β) - współczynnik nachylenia prostej wyrażony w jednostkach odchylenia standardowego;
w analizie regr wielokrotnej - pomaga ocenić, który z predyktorów ma większą siłę i jest silniej powiązany ze zmienną zależną,
czy dany predyktor wyjaśnia istotnie zmienną zależną (istotność), w jakim kierunku (dodatnim czy ujemnym) oraz jaka jest siła relacji.
Interpretacja (jak r-Pearsona, od -1 do 1): zwiększając wartość predyktora o jedno odchylenie standardowe, wartość zmiennej zależnej wzrośnie o...(beta) odchylenia standardowego,
więc po prostu patrzymy - które beta - dla ktrórego predyktora jest większe.
wartość t - weryfikacja istotności współczynników regresji (t = Beta/błąd standardowy)
- jeśli t jest nieistotny dla stałej, to nie różni się ona od zera,
a jeśli jest t nieistotne dla B - (też nie różne od zera) - wraz ze wzrostem zmiennej niezależnej
o jedną jednostkę, zmienna zależna się nie zmieni (zmieni się o zero jednostek)
7. Tabela z podsumowaniem modelu zawiera błąd standardowy oszacowania - dodajemy go do równania, gdy chcemy generalizować wyniki na populację.
Wyraża on rozbieżność my przewidywanymi wartościami a rzeczywistymi danymi (miara dokładności przewidywań).